Term Premium Estimates
|
The long-term rate associated with nominal bonds can be broken down in different ways and for different purposes. A well-known decomposition is a generalization to Fisher’s famous equation, and consist of the real interest rate, the expected inflation and the inflation risk premium. Another decomposition consists in expressing the temporary structure of interest rates as a function of a weighted sum of vectors (orthogonal to each other). This structure naturally includes the long-term interest rate, achieved through a principal component analysis. A decomposition that has regained importance in recent years is the one that allows obtaining the so-called term premium. This consists of two components: the expected average short-term interest rates and, precisely, the term premium. This decomposition has become important in the context of monetary policy. Largely, because there is a strong interest in understanding how unconventional monetary policies have affected the different components of interest rates. One possible interpretation of the expected average short-term interest rates is the long-term interest rate that would prevail if the agent was risk-neutral. The intuition is straightforward: for an agent who is risk-neutral all his risk premiums should be zero. Thus, the term premium is obtained by the estimation of the risk-neutral long-term interest rate, standardized by the interest rate. In other words, the estimation of the risk-neutral long-term interest rate allows for the identification of the term premium. Conventionally, the term premium is explained as a compensation to the holder of a long-term bond for having invested in this bond instead of having invested in short-term bonds consecutively. A more general interpretation, however, is that the term premium captures the risks for which the holder of a long-term nominal bond is compensated, namely liquidity and inflation risks. Note that, as is the case with all financial instruments, not all risks are offset, e.g., risks that are idiosyncratic to an instrument. It should be noted that some unconventional policies may affect different elements of the decomposition. For example, announcements of forward guidance by a monetary authority on keeping the short-term interest rate at one level for a given period of time should, in principle, affect the expected average short-term interest rate. Similarly, other policies may affect the term premium to the extent that they impact the risks to which the long-term bondholder is compensated. The estimation of the term premium requires an econometric model. In this case, the methodology and model proposed by Adrian, Crump, and Moench (2013, ACM) was chosen. This is due to the following reasons: That said, it is convenient to underline the following caveats. The estimation of the term premium depends on both the model and the economic variables used as inputs. In this case, an affine model of interest rates is used with interest rates at different terms as inputs. The estimate is also a function of the sample used. This is derived from the fact that interest rates are usually persistent stochastic processes. The level of the term premium is one of the statistics that are most sensitive to the choice of model, inputs, and sample used. The consideration of these caveats is especially relevant when comparing different estimates of the term premium, including those shown here. However, the dynamics of the term premium are more robust to the above-mentioned variants. Analytically, we have the following expression: |
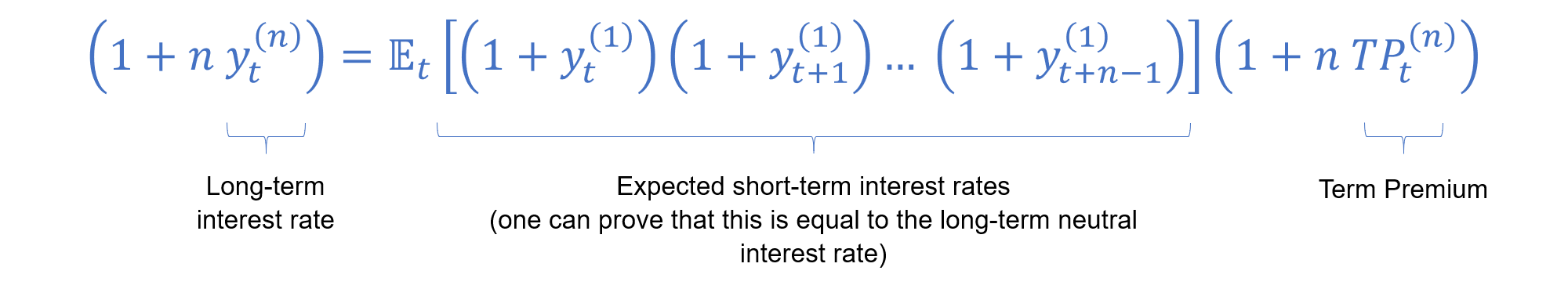
|
|
|
References for These Estimates:
LATAM:Other Useful References:
Select the countries to display the term premium estimates
|
|
|
|
|
Notes:
- The start dates of the data are: Brazil (March 27, 2007), Chile (September 29, 2005), Colombia (April 28, 2006), Mexico (January 2, 2004) and Peru (April 28, 2006). These dates depend on the availability of data for each economy.
- For our term premium estimates of Latin American economies (LATAM) we use GDP PPP-weighted averages in international dollars of our individual term premiums. LATAM: Brazil, Colombia, Chile, Mexico, and Peru. This average only considers the period for which data is available for all economies. Otherwise, there may be variations in term premium averages due to the inclusion of new series.
- The model for term premiums is re-estimated once a month. This may result in minor changes to historical estimates of the decomposition of bond rates.
- Sources: Own estimates with inputs from Bloomberg, Valmer and WEO, April 2020 for: Brazil, Colombia, Chile, Mexico and Peru. Adrian et al. (2013) for the U.S.
For daily estimates, please refer to the instructions .

